1.光谱特性图和吸收强度 (朗伯-贝尔定律)
特定波长的红外线具有被分子(原子)吸收的特性。吸收的波长根据组成分子的原子及其键合状态而变化。
下图是纵轴表示红外线吸收(透过率)、横轴表示波长(μm)的分光特性图的一例。
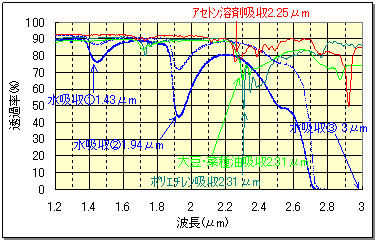
每种代表不同的特性,例如吸水特性、溶剂、薄膜和油。
另外,该吸收特性根据物质的量(厚度)而增强。
这通过以下公式表达为朗伯-比尔定律。
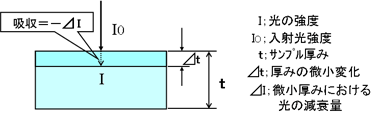
衰减量⊿I = -α・I・⊿t(α;由吸收系数、材料和波长确定的常数)
→ dI=-α・I・dt 两边按 t 积分(t=0 至 t)
红外线强度 I=I0·e^(-α·t)
Chino的红外线水分/厚度计利用该红外线吸收物质(官能团)特有的波长的特性,以及吸收量根据红外线的量(厚度)而变化的事实,来测量物质的量。我正在测量的物质中的每个成分。
2.传感器内部结构
水分、厚度计的内部构成如下所示。
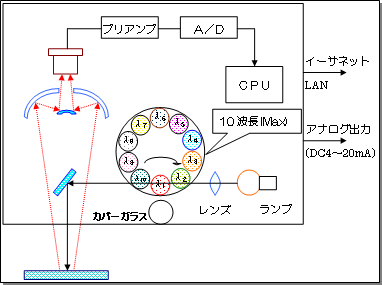
光源灯发出的光经过滤波,仅选择特定的波长,照射到材料上。照射的红外线被测量目标(官能团)的振动吸收,衰减的反射光被凹面镜重新聚焦并入射到光电探测器上。
另外,该光学滤波通过电机旋转,间歇地发射不同波长的红外线(脉冲波)。接收到的红外线由检测元件转换成电信号,将各波长数据数字化,并计算出吸光度。信号。
3.关于吸光度运算
本公司的水分、厚度计的吸光度输出主要为以下输出。
① 双波长比率运算
两个波长:吸收波长 λs 和比较波长 λr(吸收很少的参考波长)
吸光度 X= K1−λs/λr
K1;归一化常数(≒1)
② 三波长比率运算
使用两个波长:吸收波长 λs 和比较波长 λr1 和 λr2。
吸光度 X = K1-λs/(α·λr1+(1-α)·λr2)
K1:归一化常数(≒1),α:波长加权常数(0<α<1)
③ 多元回归运算
机载红外线的波长为λ1~λn,由于吸收特性呈指数关系,因此各波长数据的对数用下式计算。
分量值 Y=a0+a1・Log(λ1)+a2・Log(λ2)+...an・Log(λn)
(水分、厚度、溶剂等)
①中的二波长比计算,通过吸收量与吸收量的比值,计算出因外界光、测量距离、光路灰尘、表面状况波动等干扰因素而引起的光量的绝对值。这样做的优点是可以尽可能减少引起波动的干扰。
另外,②中描述的3波长比计算是2波长方法的高级版本,在处理样品表面状况、颜色、含量成分比例等方面的差异方面具有很强的优势(我们将这种差异称为质地)。
在使用比率计算的吸光度计算方法中,使用该吸光度创建校准曲线并计算所需成分值。
在③中的多元回归计算中,如果确定了该方程的系数,则可以输出直接计算的分量值。当要寻找的成分不是用单一的变化量(一个吸收波长)表示,而是受到多个(水分和厚度的吸收波长)影响(干扰)时,使用这种多元回归计算,每个元素这种计算方法是通常用于处理多元变量时的统计数学处理。为了找到这个多元回归计算的系数,我们应用测量值并以联立正规方程的形式找到它们。
此外,当同时测量多个成分时,通过将该多重回归计算的系数应用于每个成分,可以同时测量水分和厚度。
4.关于校准曲线
这是根据第3节①和②中确定的2(水分%、厚度μm、溶剂%等)的变化而增加或减少的变量,而不是成分本身的量。
需要校准曲线来确定获得该吸光度值所需的组分量。
校准曲线是预先用水分/厚度传感器在测量范围内的几个级别测量样品,并使用最小二乘法计算吸光度值(X值)和实际测量数据(误差较大)这是使用寻找减少 的回归公式的方法获得的公式。
<校准曲线数据>
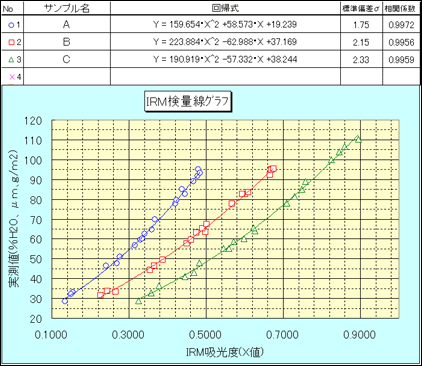
校准曲线基本上是为每种产品类型创建的。该传感器最多可存储99条校准曲线,每次产品类型改变时可切换校准曲线通道。
*
链接到如何计算回归公式、标准差和相关系数
参考资料1.关于标准曲线数据与基于兰伯特-贝尔定律的吸光度值的关系
在前一节中的校准曲线数据中,测量值Y和通过2(3)波长比计算确定的吸光度X值之间的关系是使用一阶至三阶多项式确定的。另一方面,朗伯-比尔定律使用对数对数计算来计算吸光度的公式(当求解厚度t时,t=-(1/α)·Log(I)+β)。
以下是使用基于朗伯-比尔定律的理论公式计算出的吸光度和使用本公司使用的“2波长比计算”进行二次或三次回归计算的厚度测量示例。显示了两种情况之间的关系。在下图中。
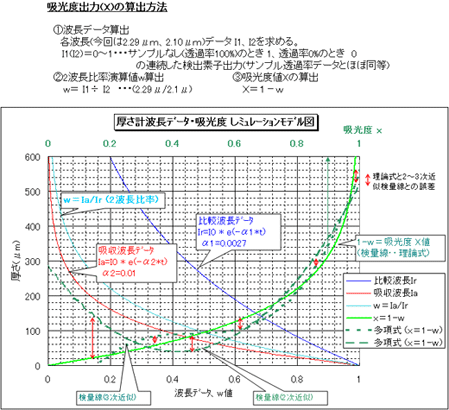
在这个模型示例中,图中的红色箭头表示与理论公式的误差。
但实际上,每种类型(批次)的测量范围在一定程度上是确定的,通过在该范围内进行详细的回归计算,可以将误差减小到不会对使用造成问题的程度。 。
另外,对于多元回归计算,计算每个波长数据的对数(Logλn),与理论公式的计算方法相同,因此进一步提高了回归计算的准确性。
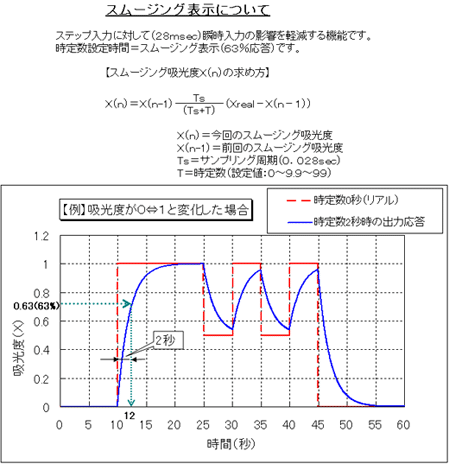
参考资料2.关于平滑运算
本公司的水分、厚度计主要用于在线测量。在线测量时,由于各种外来干扰光、测量距离、光路上的粉尘、表面状态的变动等,测量数据会出现波动。因此,本公司进行如下运算处理,消除这些干扰,实现稳定的测量。